Creating my own spreadsheet to convert binary to decimal
About this lesson
A spreadsheet can be used to do calculations quickly using formulas. How can we make a spreadsheet that converts a binary number to a decimal number? This lesson provides some guidance and Excel files for student and teacher use.
Year band: 5-6, 7-8
Curriculum Links AssessmentCurriculum Links
Links with Digital Technologies Curriculum Area
| Strand | Content Description | |
|---|---|---|
| Years 5-6 | Knowledge and Understanding |
explain how digital systems represent all data using numbers |
| Years 7-8 | Knowledge and Understanding |
explore how data can be represented by off and on states (zeros and ones in binary) |
Links with Mathematics Curriculum Area
| Strand | Content Description | |
|---|---|---|
| Year 5 | Number |
Solve problems involving multiplication of larger numbers by one- or two-digit numbers, choosing efficient calculation strategies and using digital tools where appropriate; check the reasonableness of answers (AC9M5N06) |
| Year 6 | Algebra |
Recognise and use rules that generate visually growing patterns and number patterns involving rational numbers (AC9M6A01) |
ICT Capability
Typically, by the end of Year 6, students:
Generate solutions to challenges and learning area tasks
- identify the risks to identity, privacy and emotional safety for themselves when using ICT and apply generally accepted social protocols when sharing information in online environments, taking into account different social and cultural contexts
Typically, by the end of Year 8, students:
Generate solutions to challenges and learning area tasks
- design and modify simple digital solutions, or multimodal creative outputs or data transformations for particular audiences and purposes following recognised conventions.
Assessment
You can use this matrix to help assess the activity which is based on the solo taxonomy.
|
Creating a binary number converter |
||||
|---|---|---|---|---|
| SOLO LEVEL | One | Many | Relate | Extend |
| SOLO VERB |
Identify & Define |
Combine & Perform Serial Skills |
Apply |
Create & Evaluate |
| Success Criteria |
I can identify the binary digits as 0 and 1 |
I can calculate the decimal equivalent of an 8-bit number |
I can modify or create a basic binary calculator that converts an 8-bit binary number to its decimal equivalent using a spreadsheet |
I can design a Binary converter and evaluate its effectiveness |
| Digital Technologies Way Of Thinking |
|
Computational Thinking |
Computational Thinking |
Design Thinking |
Suggested steps
Prior knowledge
To undertake this activity there is an expectation that students have an understanding of binary numbers and how to count in binary. Refer to the introduction to binary lesson.
A quick revision
Revise what students know about counting in binary, if possible use binary cards or write a decimal number on the board eg ‘21’ to model how to represent that number in binary, which is 10101. Use the following table with headings to show the progression of the binary numeral system much like 1s, 10, 100, 1000 for decimal system. Binary is a doubling pattern of 1, 2, 4, 8, 16 etc.
Use the table to ensure all students can count in binary and represent decimal numbers in binary.
| 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Note remember to start from the left when using the table to make a decimal number. For example to make the number 21 do I need a 16, YES. Do I need and 8, NO. Do I need a 4, YES. Do I need a 2, NO. Do I need a 1, YES. So the binary number is 10101. Repeat this process for other numbers. Try making numbers 1-21. Ask what the largest number than can be made in this table.
Numbers larger than 21. If we add another column how can we make the number 43?
| 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
How can we make the number 251? Discuss the pattern of doubling to get 64 and 128 and add these two new columns.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
Creating a spreadsheet
Differentiate the task depending on your student’s familiarity and skills using a spreadsheet. Scaffold the learning by providing a spread sheeting file which has the set up partly completed. The files provided are MS Excel.
Some students who are well skilled in using a spreadsheet can design their own converter and may not need a file to scaffold their learning.
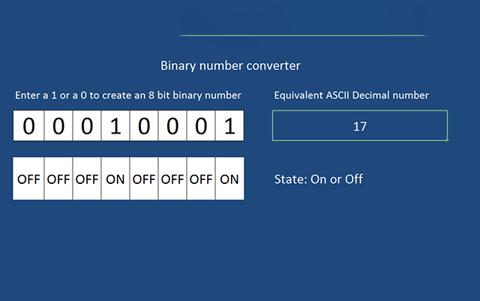
Provide this file (Binary to decimal converter file - easy) for students that have a basic understanding of how to use a spreadsheet. As a starting point ask students to test the sheet to see how it operates. Can they work out how the ASCII decimal number is calculated? Ask students if they can make their converter work up to the decimal number of 255. Encourage students to test and check to see if auto sum is correct and outputs in the cell as the correct ASCII Decimal Number.
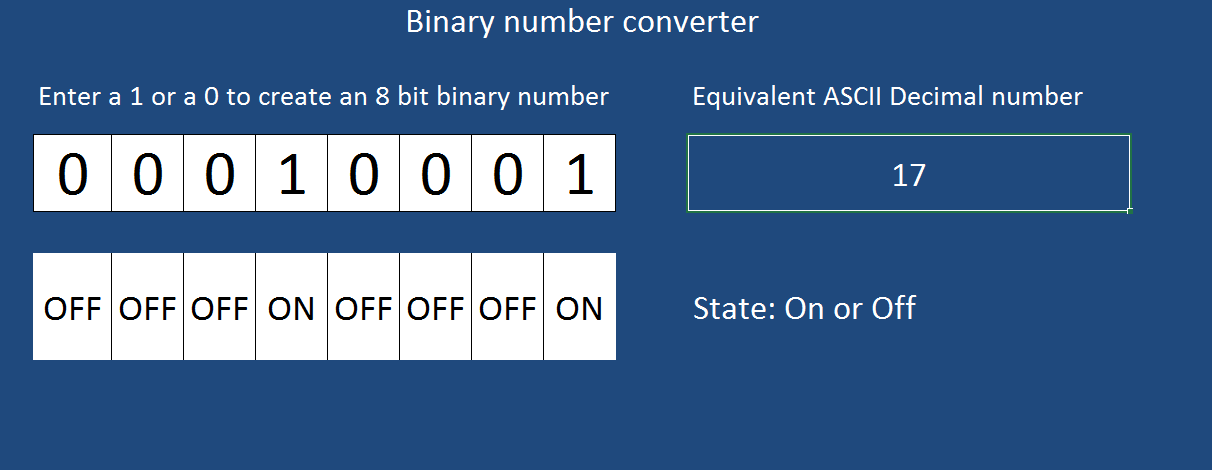
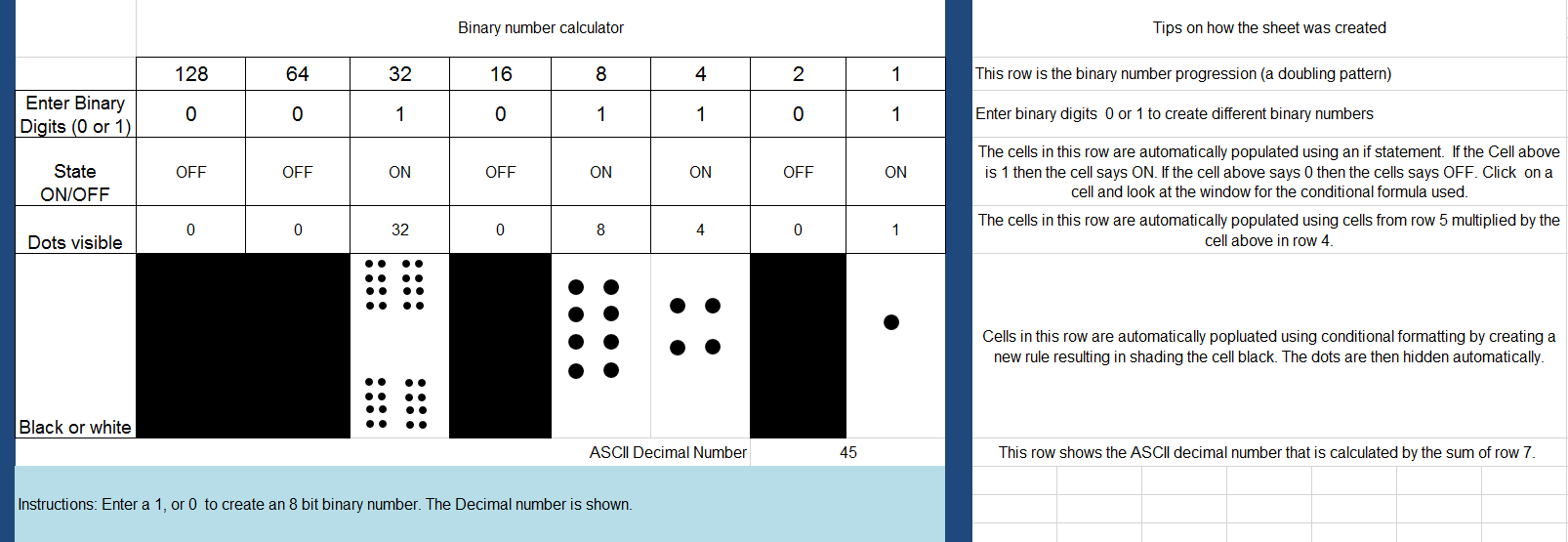
For students who want to add a conditional if statement to automatically represent o or 1 as on or off, use this file (Binary to decimal converter file - conditional). In this example the conditional statement reads if cell (above) = 1 then show On, else if cell = 0 show Off.

A completed version might look similar to this, see the file here (Binary to decimal converter file - conditional completed).
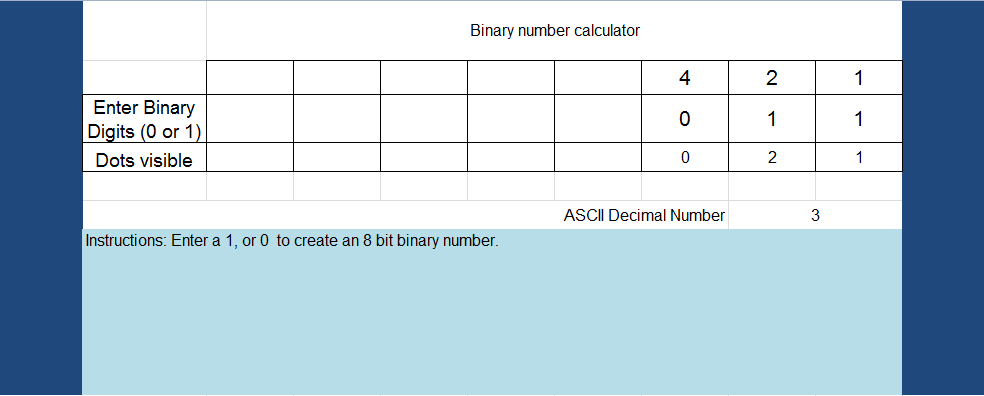
For students that are interested in creating an interface refer to this example.
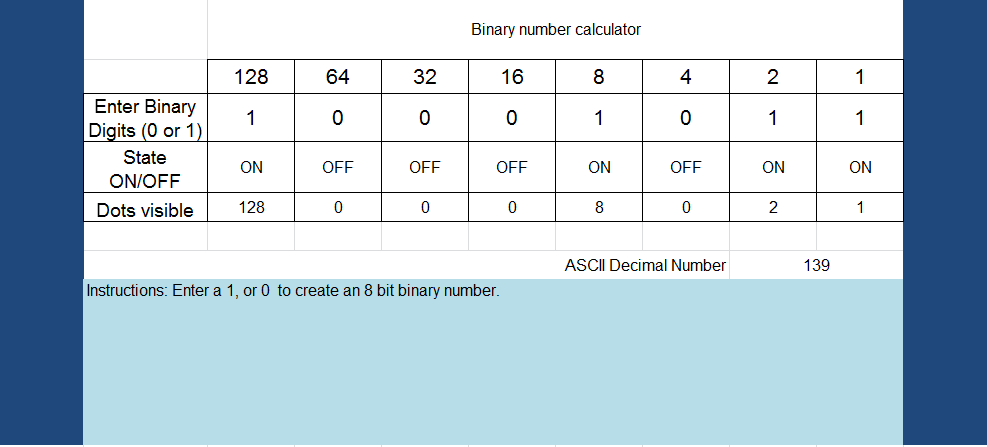
Refer to this version (Binary to decimal converter - full version with tips) of the completed spreadsheet with tips that explain how the sheet is set up.
This version includes binary cards with dots, which can be used as a further challenge.
Why is this relevant?
Computers today use the binary system to represent information. It is called binary because only two different digits are used. It is also known as base two (normally we use base 10). Each zero or one is called a bit (binary digit). A bit is usually represented in a computer’s main memory by a transistor that is switched on or off, or a capacitor that is charged or discharged.
One bit on its own can’t represent much, so they are usually grouped together in groups of eight, which can represent numbers from 0 to 255. A group of eight bits is called a byte.