Introduction to binary

About this lesson
This sequence of lessons focuses on what a binary number is, what a decimal number is, why binary numbers are important in digital systems and how to read and understand a binary number.
Year band: 5-6, 7-8
Curriculum Links AssessmentCurriculum Links
Links with Digital Technologies Curriculum Area
| Strand | Year | Content Description |
|---|---|---|
| Knowledge and Understanding | 5-6 |
Explore how data can be represented by off and on states (zeros and ones in binary) (AC9TDI6K04). |
| Knowledge and Understanding | 7-8 |
Investigate how digital systems represent text, image and audio data using integers |
Links with other Learning Areas
| Learning Area | Year | Strand and Content Description |
|---|---|---|
| Mathematics | 5-6 | Number Use solve problems involving multiplication of larger numbers by one- or two-digit numbers, choosing efficient calculation strategies and using digital tools where appropriate; check the reasonableness of answers (AC9M5N06) |
| 7-8 | represent natural numbers as products of powers of prime numbers using exponent notation (AC9M7N02) |
Assessment
Throughout working time, observe student progress and make anecdotal notes based on the learning intentions of the lesson:
- what a binary number is,
- what a decimal number is (revision)
- why binary numbers are important in digital systems
- how to read and understand a binary number.
Student work samples from the maths workbook (learning construction section) and the KWL chart could also be collected for assessment records.
Learning hook
- Prior to showing the video, ask students to write what they know about binary numbers in the Knowledge column of the KWL Chart. If you have access to collaborative writing tools like Google Docs or Microsoft 365, you could do this together online. Or try using a class Padlet to complete the KWL chart together.
- Show students James May’s video about binary numbers (James May's Q&A). Throughout the video, encourage students to note any questions (Wondering column) or new knowledge (Learning column) they have about binary or decimal numbers. Ask students to share questions, or any ideas they have learned from the short film. Keep track of all contributions.
Learning map and outcomes
Briefly discuss the learning intention of the lesson with students.
For example:
Today, we are going to learn:
- what a binary number is,
- what a decimal number is (revision)
- why binary numbers are important in digital systems
- how to read and understand a binary number.
Students have a clear understanding of what they are hoping to achieve in this lesson.
Learners could discuss the different skillsets and mindsets they will have to adopt ‐ this ties in with the Creative and Critical Thinking Capabilities.
Learning input
Whole class activity
- As a whole class, step through the following Presentation Slides [PDF/PPT] both PDF and PPT. Provide sufficient time for students to work through the challenges. Share answers as students progress.
- Begin with the initial two slides. Revisit the principles of binary numbers explained in the James May video. Compare decimal numbers (base 10) and binary numbers (base 2).
- Work through the examples in the slides of how students convert numbers from binary into decimal. Highlight that this conversion relies on users adding numbers to determine the equivalent decimal number.
- Send students back to their desks to complete Stage 1 of the ‘Learning construction’ section below.
Learning construction
- Give students a binary chart and spare 0s and 1s to cut up (Binary Table and Numbers pdf).
- Give students the Stage 1 binary number cards (Stage 1 Creating a decimal number from a binary number – numbers for working time pdf) so that they can create decimal numbers from binary numbers.
- This activity has a range of ability levels to choose from. You can provide the different levelled numbers for the students. Alternatively, students can self-select.
- When complete, correct as a whole class, enabling students to ask questions if they encounter an incorrect answer.
Learning demo
Group challenge
In small groups, students race to complete the challenge the fastest.
- Give out the challenge cards (Stage 1 Creating a decimal number from a binary number – challenge cards pdf).
- In teams, students work together to convert five binary numbers into decimal numbers. When complete, the group shouts ‘stop’ and receives a time.
- Students swap responses with another group and correct answers. You could complete a short reflection here and ask how successfully the teams collaborated. Did everyone participate equally? Did they devise a strategy to complete this challenge?
- Alternatively use these online binary cards for a binary number of 8 digits (byte) provided by CS unplugged. As a starting point you may want to use 5 online binary cards which make it easier to introduce the concept. Do this by typing '5' in the 'Cards to show' section of the CS unplugged site.
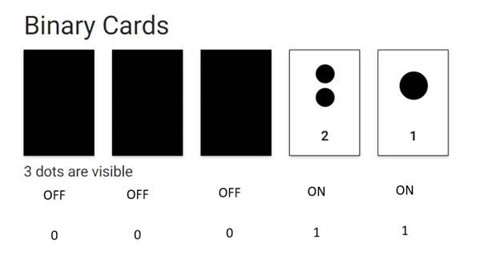
Learning reflection
- Provide students with three quick questions to answer prior to leaving.
Do an eyes-closed hands-up traffic-light poll. (Ask students to hold up three fingers if they understand the concept well enough that they could teach it; two fingers if they think they understand it, but only just; and one if they need help).Questions:
- Do you understand what a binary number is?
- Do you understand why binary numbers are important in digital systems?
- Can you read and understand a binary number?
- Can you convert a binary (base 2) number to a decimal (base 10) number?
- Make anecdotal notes of any students who do not reply ‘yes’ to these questions.
Revisit the skills and mindsets you discussed at the start of the lesson. What examples of great learning behaviours did we see? How could we be even more effective learners?